Clock
-
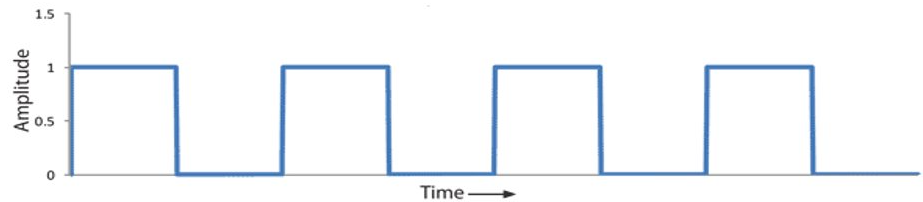
The clock is a system signal, usually a square wave; that acts as the heartbeat to a computer system.
-
All operations in a computer system are synchronised using the systems clock.
-
Generally, the system clock’s period is longer than the switching time of the system. (It could work as
Oscillator)
Timing Diagrams
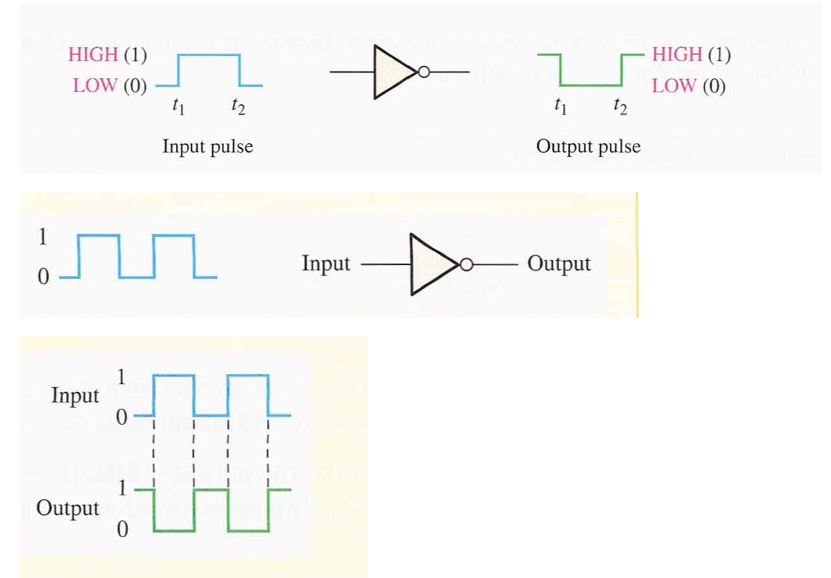
A timing diagram shows how two or more waveforms relate in time
Fundamental Logic Types: AND
Boolean Equation:
| A | B | S | |
|---|---|---|---|
| 0 | 0 | 0 | |
| Truth Table | 0 | 1 | 0 |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
All inputs must be '1'. Code symbol is two ampersands -> &&.
e.g., MFA
Real life Example using AND Gate
Consider a motorised gate that opens only under specific conditions:
- Input A: Status of the security card reader (1 for a valid card, 0 for an invalid card).
- Input B: Status of the PIN entry (1 for correct PIN, 0 for incorrect PIN).
- Output S: Overall status of the gate, indicating whether it should open or not.
The Boolean equation for this scenario is:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
In this setup, the motorized gate would open only when both conditions of a valid security card and a correct PIN are met, utilizing the logic of the AND gate.
Fundamental Logic Types: OR
Boolean Equation:
| A | B | S | |
|---|---|---|---|
| 0 | 0 | 0 | |
| Truth Table | 0 | 1 | 1 |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
EIther input must be '1'. Code symbol is two pipes -> ||.
Security System Example using OR Gate
Consider a security system for a building with two sensors:
- Input A: Status of the main entrance door sensor (1 for open, 0 for closed).
- Input B: Status of the window sensor (1 for broken, 0 for intact).
- Output S: Overall alarm status.
The Boolean equation for this scenario is:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
In this setup, the alarm is triggered if either the main entrance door is opened or the window is broken
Universal : NOR
Boolean Equation:
| A | B | S | |
|---|---|---|---|
| 0 | 0 | 1 | |
| Truth Table | 0 | 1 | 0 |
| 1 | 0 | 0 | |
| 1 | 1 | 0 |
No inputs must be '1'. Code symbol is a exclamation mark and pipe -> !|.
Burglar Alarm System Example using NOR Gate
Consider a burglar alarm system in a building that is armed when neither the motion sensor nor the door sensor is triggered:
- Input A: Status of the motion sensor (1 for triggered, 0 for not triggered).
- Input B: Status of the door sensor (1 for open, 0 for closed).
- Output S: Overall status of the burglar alarm, indicating whether it should be armed or not.
The Boolean equation for this scenario is:
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
In this setup, the burglar alarm system would be armed only if neither the motion sensor nor the door sensor is triggered.
Universal: NAND
Boolean Equation:
| A | B | S | |
|---|---|---|---|
| 0 | 0 | 1 | |
| Truth Table | 0 | 1 | 1 |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
All inputs must be '1'. Code symbol:
!( foo && bar )
Security Access System Example using NAND Gate
Consider a security access system where a door lock remains locked only if both a key card and a PIN code are incorrect:
- Input A: Status of the key card (1 for correct, 0 for incorrect).
- Input B: Status of the PIN code (1 for correct, 0 for incorrect).
- Output S: Overall status of the door lock, indicating whether it should remain locked or be released.
The Boolean equation for this scenario is:
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
In this setup, the door lock remains locked only if both the key card and the PIN code are incorrect.
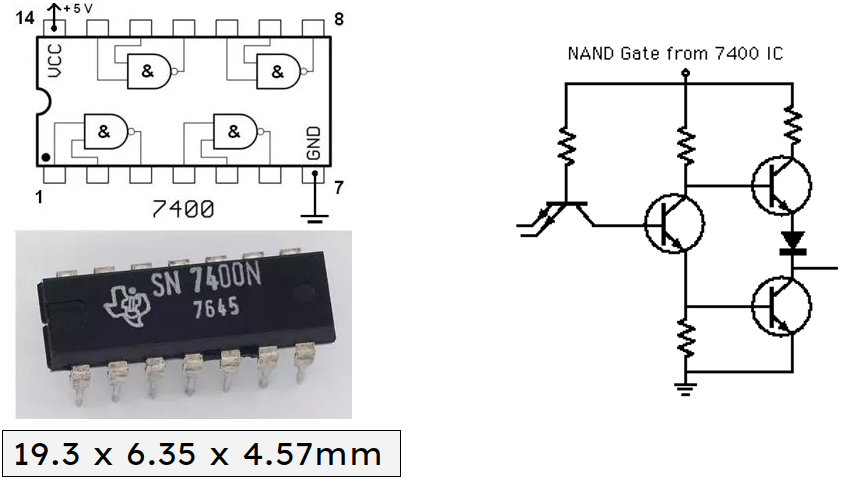
NAND Integrated Circuit
XOR Gate
Boolean Equation:
| A | B | S | |
|---|---|---|---|
| 0 | 0 | 0 | |
| Truth Table | 0 | 1 | 1 |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
All inputs must be '1'. Code symbol is a hat (only for comparison) -> ^.
Smart Home Security System Example using XOR Gate
A security camera is triggered to record only when either motion is detected outside or an authorized person enters a correct PIN code:
- Input A: Status of the motion sensor (1 for motion detected, 0 for no motion).
- Input B: Status of the PIN entry (1 for correct PIN, 0 for incorrect PIN).
- Output S: Overall status of the security camera, indicating whether it should be triggered to record or not.
The Boolean equation for this scenario is:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
In this setup, the security camera is triggered to record only when either motion is detected outside or an authorized person enters a correct PIN code.
Transistors
- Transistors are fundamental components in implementing digital circuits and logic operations.
- Transistors are semiconductor devices that can be used to amplify or switch electronic signals.
Menti: Which logic gates are correctly labelled?
Or go to menti and use this code (5442 0426)
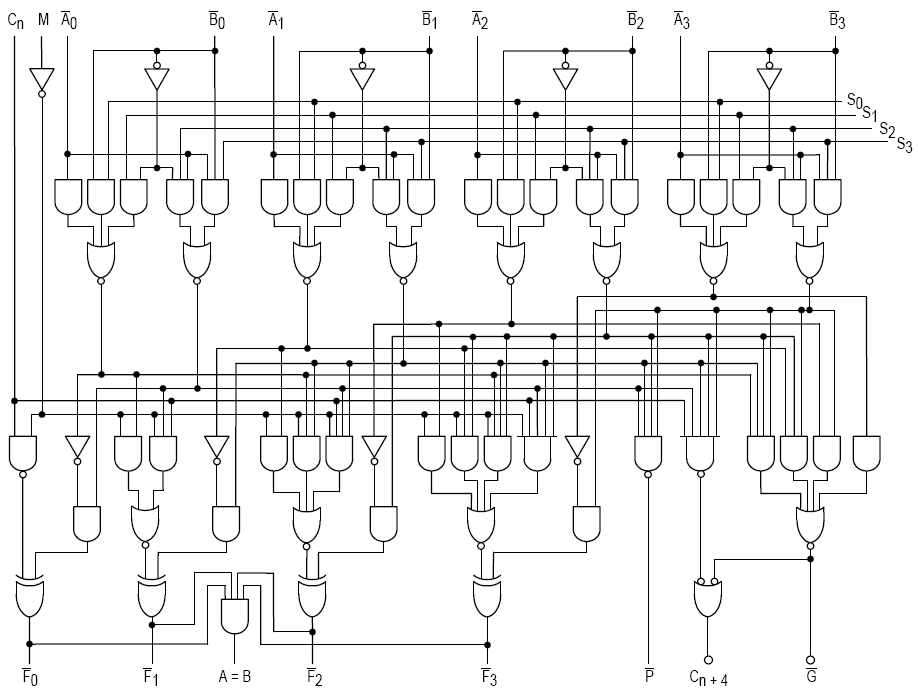
Arithmetric Logic Unit (ALU)
The ALU adds binary numbers that are positivily or negatively signed in combinations to perform addition, multiplication, subtraction and division.
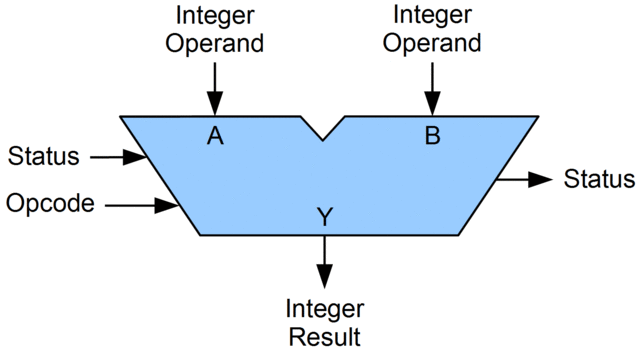
This is all done with logic gates in a circuit called an adder.
Binary Addition
| Binary A | Binary B | Sum (Binary) | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
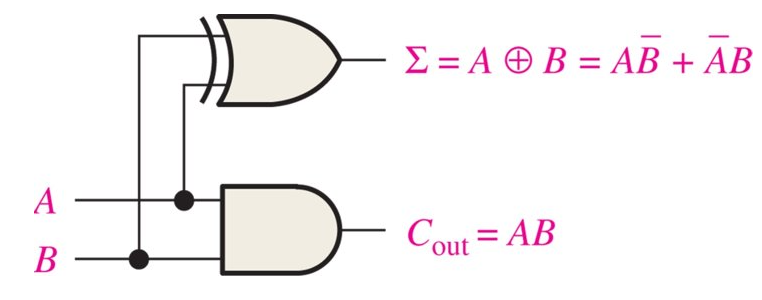
Half Adder
Logic symbol for a Basic calculator or half added
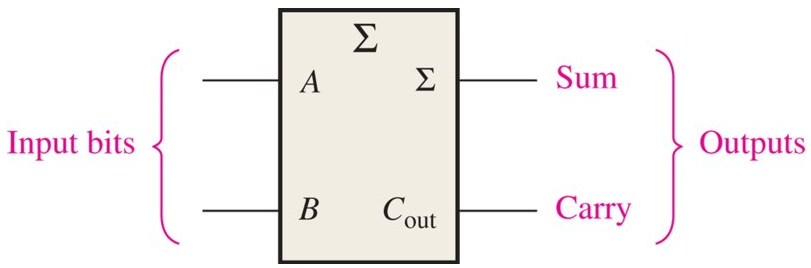

Sum (RED)
XORCarry (RED)
ANDHalf adder Logic Diagram
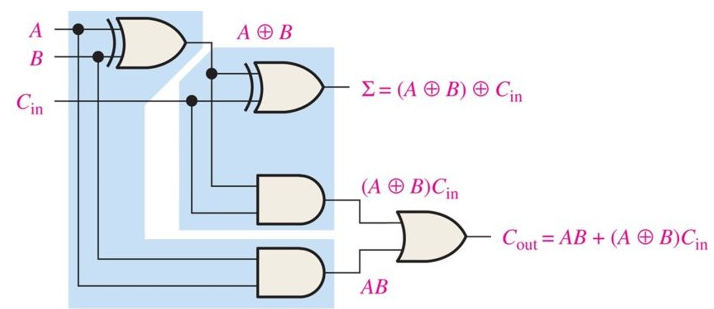
Full Adder
| Binary A | Binary B | Carry In | Carry Out | Sum (Binary) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
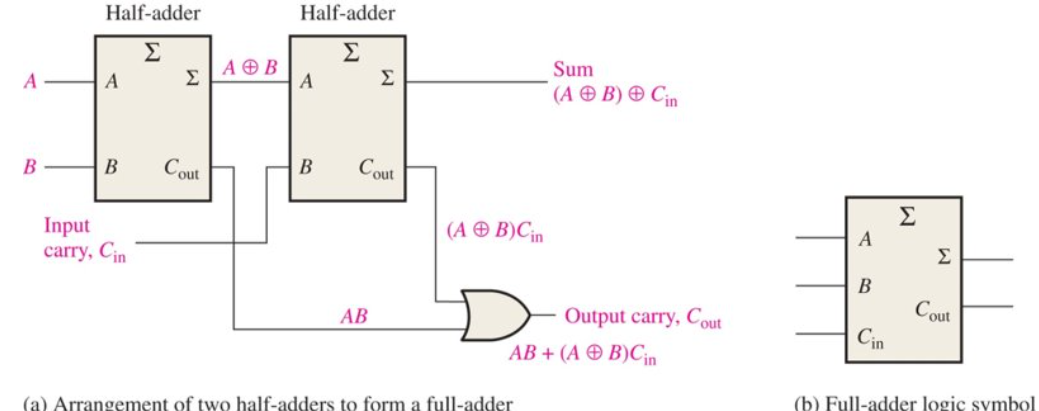
Full Adder
Full Implemented with Half Adders
ALU Logic Circuit
Labs (Logic Sim )
-
Walkthrought lab is here
-
And we will be using Logic Simulator