Intended Learning Outcomes

1. Calculate simple Boolean equations​

2. Explain the difference between Sum of Products and Standard Sum of Products.

3. Recall Boolean Algebra Laws

4. Recall how to minimise the terms.​

Boolean Logic

In Boolean algebra, a variable is a symbol is used to represent an action, a condition, or data. A single variable can only have a value of 1 or 0. ​

The complement represents the inverse of a variable and is indicated with an overbar. Thus, the complement of is .​

​
A literal is a variable or its complement.​

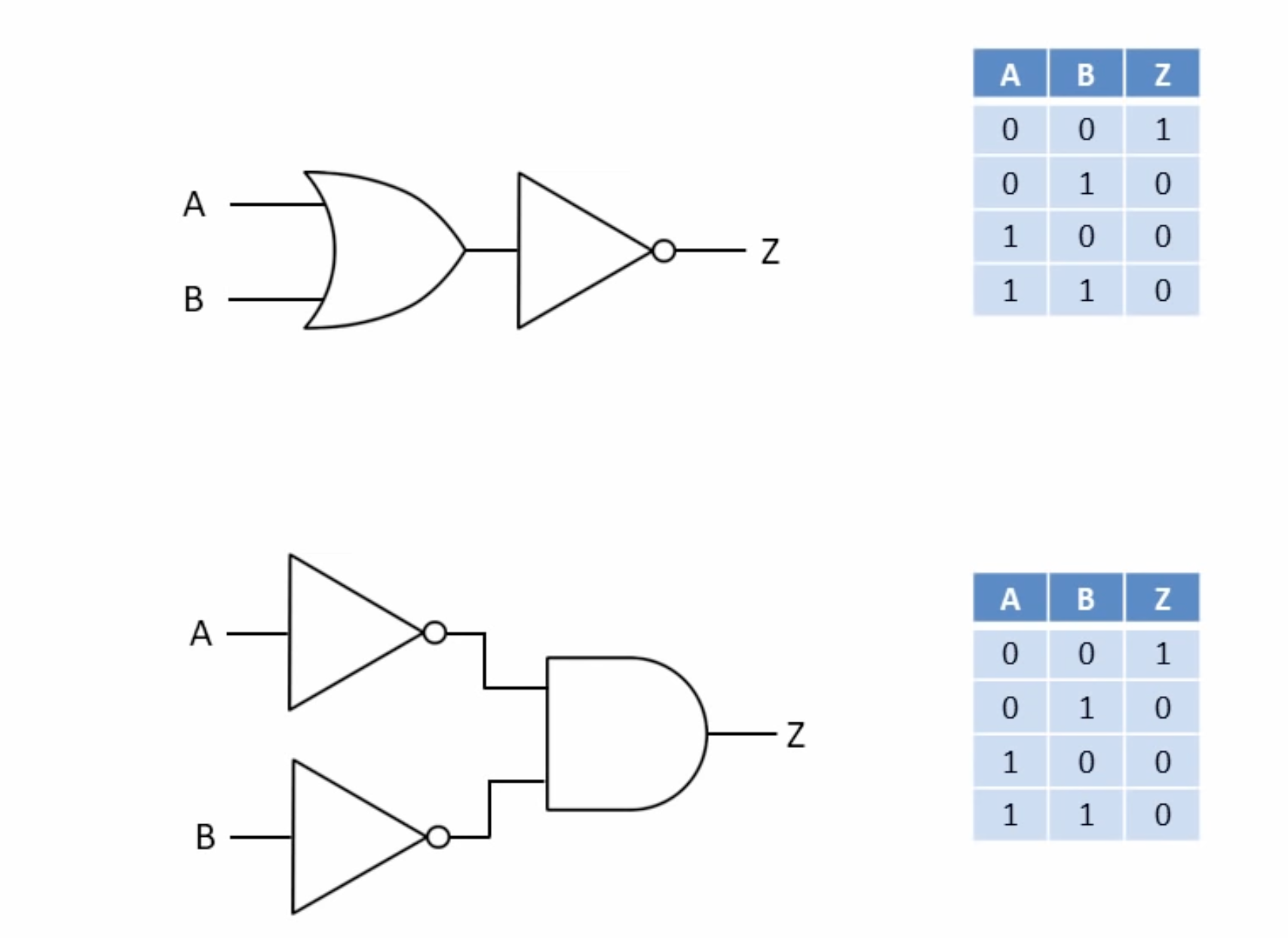
Boolean Addition

There can only be or .​

Boolean Addition/Sum

Parallel Switch

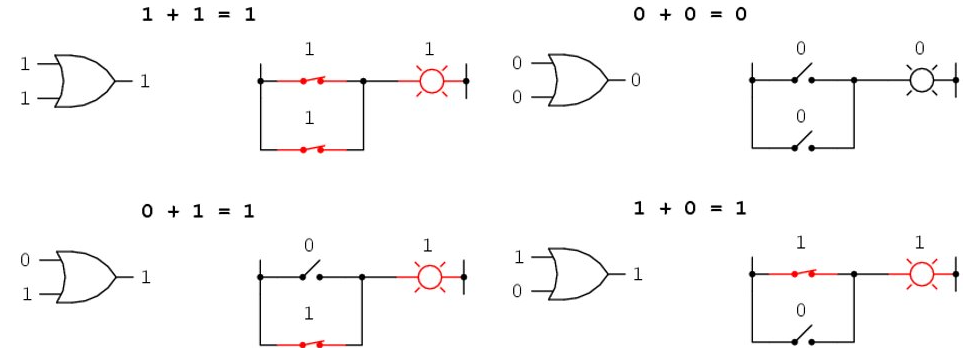
Boolean Vs Binary Addition

It does not matter how many or few terms we add together, either. ​

​Consider the following sums:​

But in binary addition:

Boolean Sum Term

• In Boolean algebra, a sum term is a sum of literals. ​

• In logic circuits, a sum term is produced by an OR operation with no AND operations involved. ​

Some examples of sum terms are:​

• A sum term is equal to when one or more of the literals in the term are . ​

• A sum term is equal to only if each of the literals is .​

Sum Example

A sum term is a sum of literals. The sum term is 1 if one or more of the literals are 1. ​

The sum term is zero only if each literal is 0.​

​Determine the values of ‘A’, ‘ B’, and ‘C’ that make the sum term of the expression:​

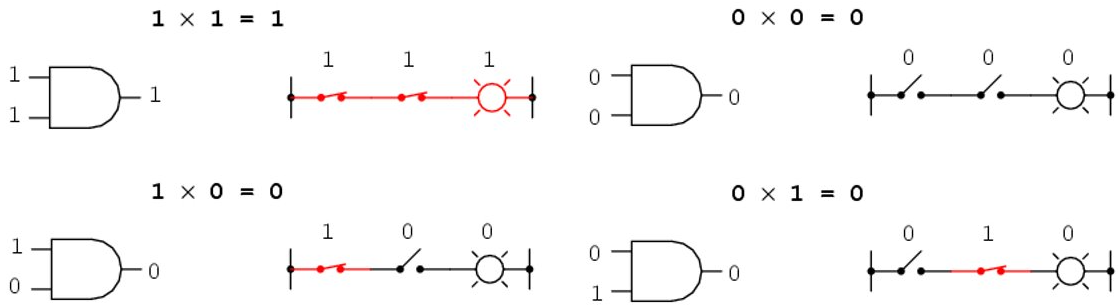
Boolean Multiplication

Series Switch

Product Term "MINTERM"

In Boolean algebra, a product term or “minterm” is the product of literals. ​

In logic circuits, a product term is produced by an AND operation with no OR operations involved. Some examples of product terms are ​

A product term is equal to 1 only if each of the literals in the term is 1. A product term is equal to 0 when one or more of the literals are 0.​

Product Term Example

A product term is the product of literals.​

Determine the values of ‘A’, ‘ B’, and ‘C’ that make the sum Product term of the expression:​

Sum-of-Products (SOP) Terms

When two or more product terms are summed by Boolean addition, the resulting expression is a sum-of-products (SOP). Some examples are:​

Legal SOP Expression:

ILegal SOP Expression:

AND / OR Implementation of an SOP Expression

Liteals SOP

Standard SOP (SSOP)

When all input variables appear in each product term, the expression is known as a standard Sum of Product (SOP) expression:

Following expression has input variables A, B, C and D , complete set of variables is not present in the first two expression ​

Following is a standard SOP (SSOP) expression​

Output of a digital circuit written as SSOP

Standard Sum of Product Example

Only the product terms where circuit produces 1 (values of S) are added in the equation

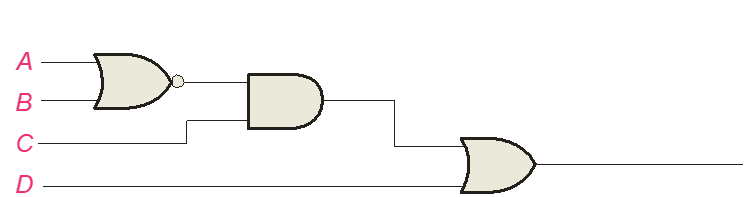
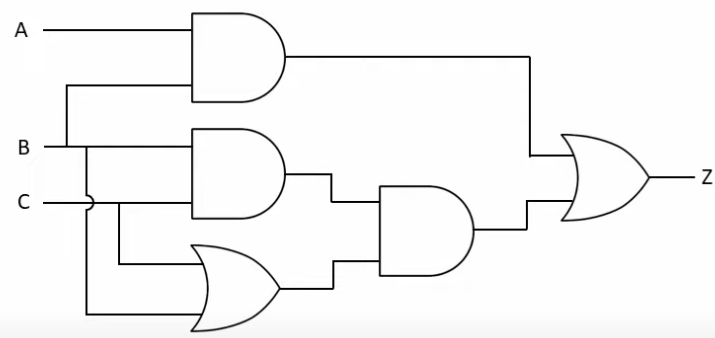
Boolean Analysis of Logic Circuits

Combinational logic circuits can be analyzed by writing the expression for each gate and combining the expressions according to the rules for Boolean algebra.​

Apply Boolean algebra to derive the expression for X.​

Write the expression for each gate:​

Grouping in AND

Simpler AND gates in Groups produce the same output of a big complex AND gate.​

Grouping in AND

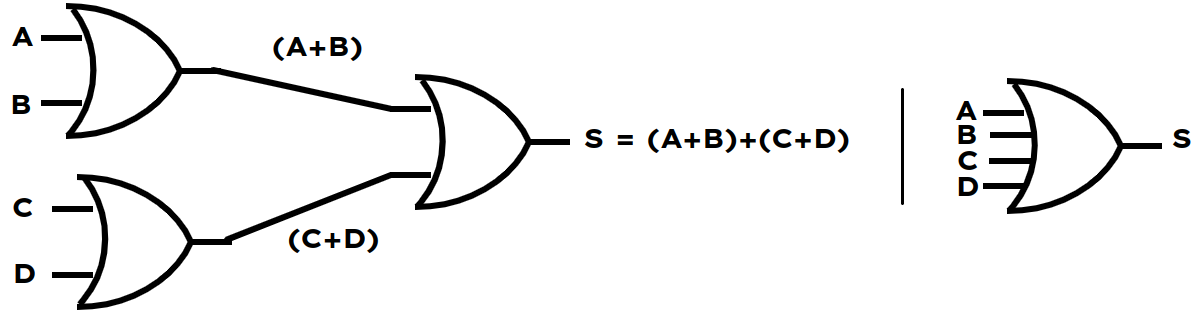
Simpler AND gates in Groups produce the same output of a big complex OR gate.​

End of Morning Session

• See you at 13:00 VH2.04 (a,b,c)

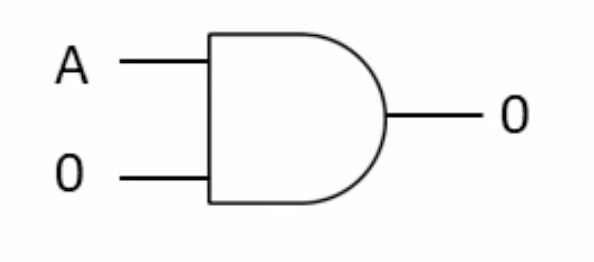
1- Basic Rules (Annulment (Null) Law)

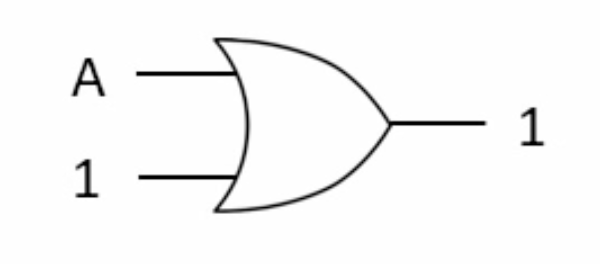
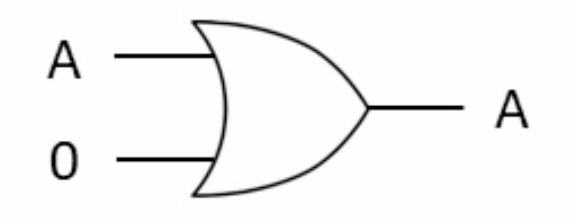
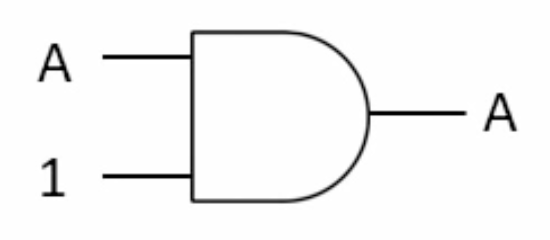
2- Basic Rules (Identity Law)

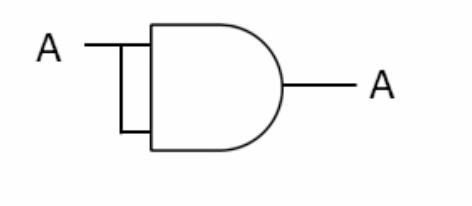
3- Basic Rules (Idempotent Law)

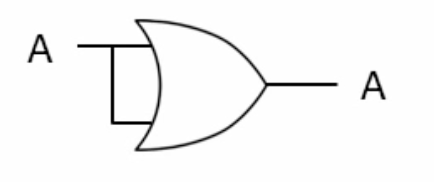
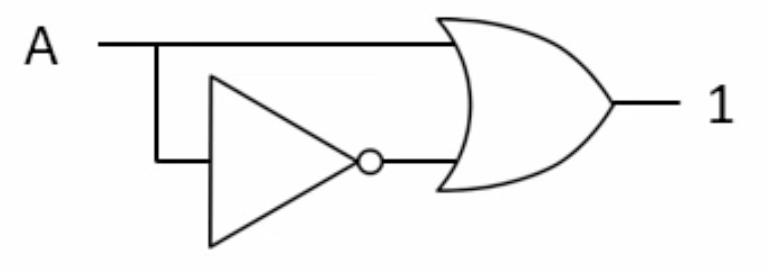
4- Basic Rules (Complement Law)

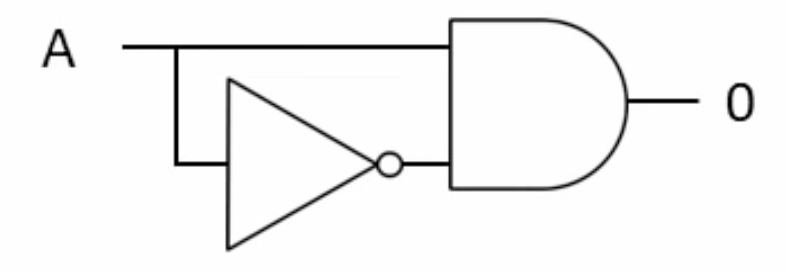
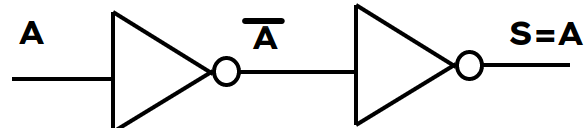
5- Double Negation

Note we see that a double inversion, cancel each other out!

Boolean Equation :

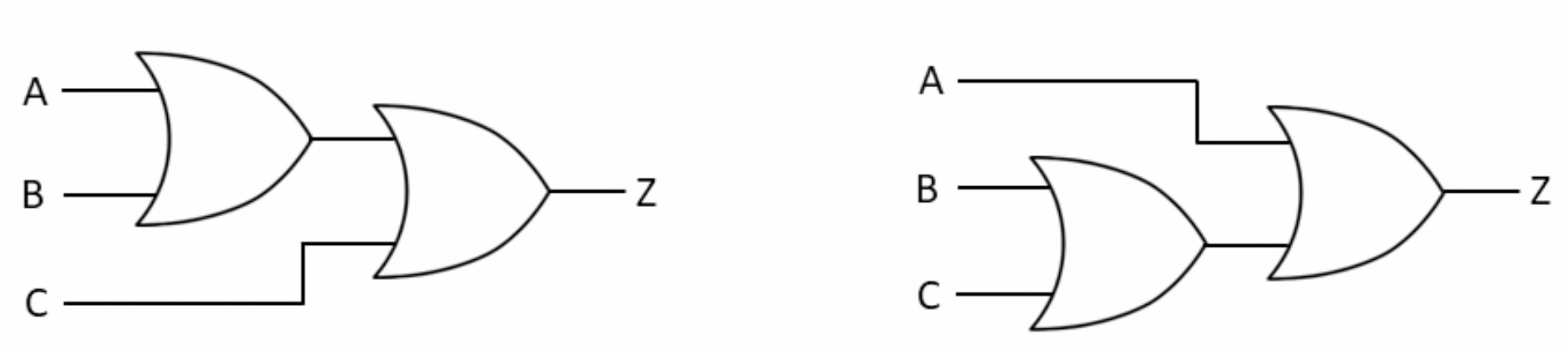
6- Associative Law

The associative laws are also applied to addition and multiplication. For addition, the associative law states​

When OR’ing more than two variables, the result is the same regardless of the grouping of the variables.​

For multiplication, the associative law states​

When ANDing more than two variables, the result is the same regardless of the grouping of the variables.​

Example:

Z= (A.B).C == A.(B.C)

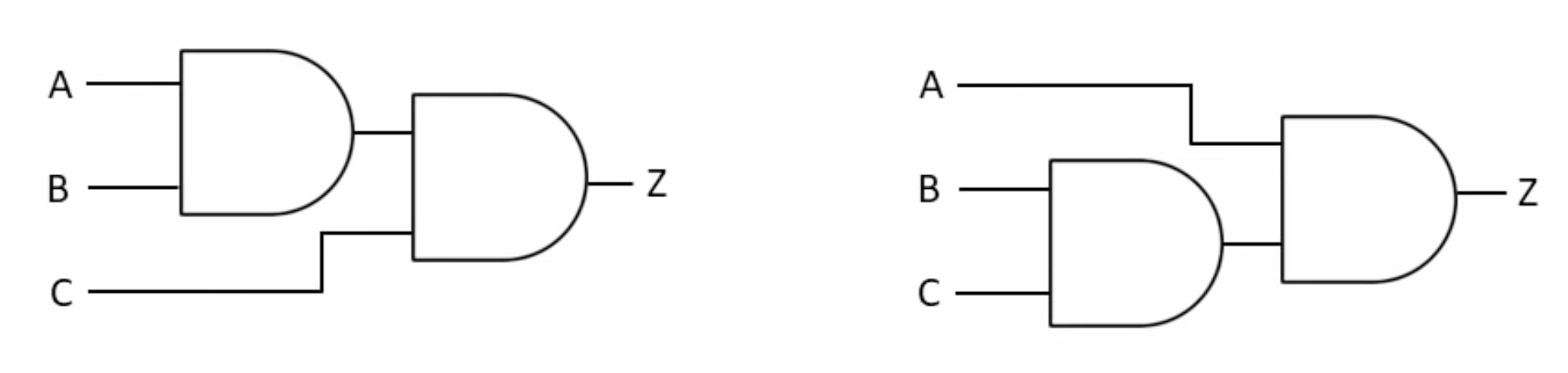
Z= (A+B)+C == A+(B+C)

7- Commutative Law

The commutative laws are applied to addition and multiplication. For addition, the commutative law states:​

In terms of the result, the order in which variables are ORed makes no difference.​

For multiplication, the commutative law states:​

In terms of the result, the order in which variables are ANDed makes no difference.​

8- Distributive Law

The distributive law is the factoring law. A common variable can be factored from an expression just as in ordinary algebra. That is​

The distributive law can be illustrated with equivalent circuits:​

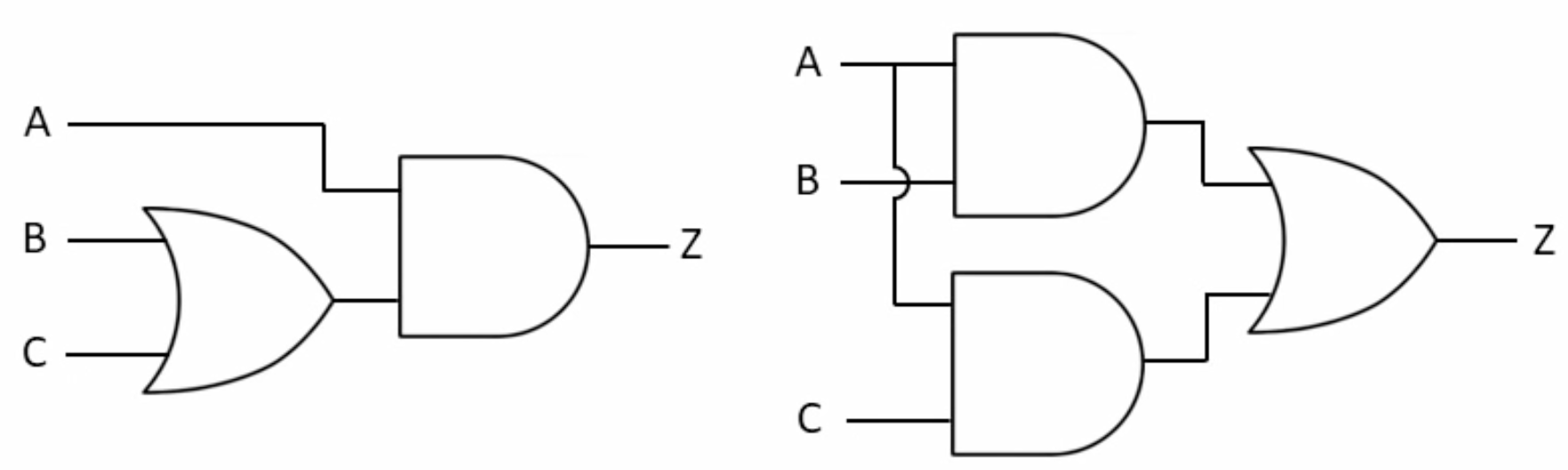
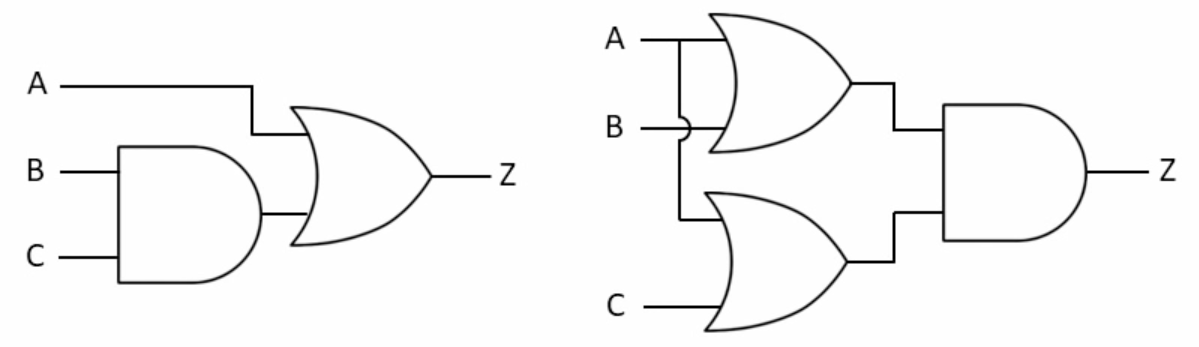
9- Absotptive (Redundancy ) Law

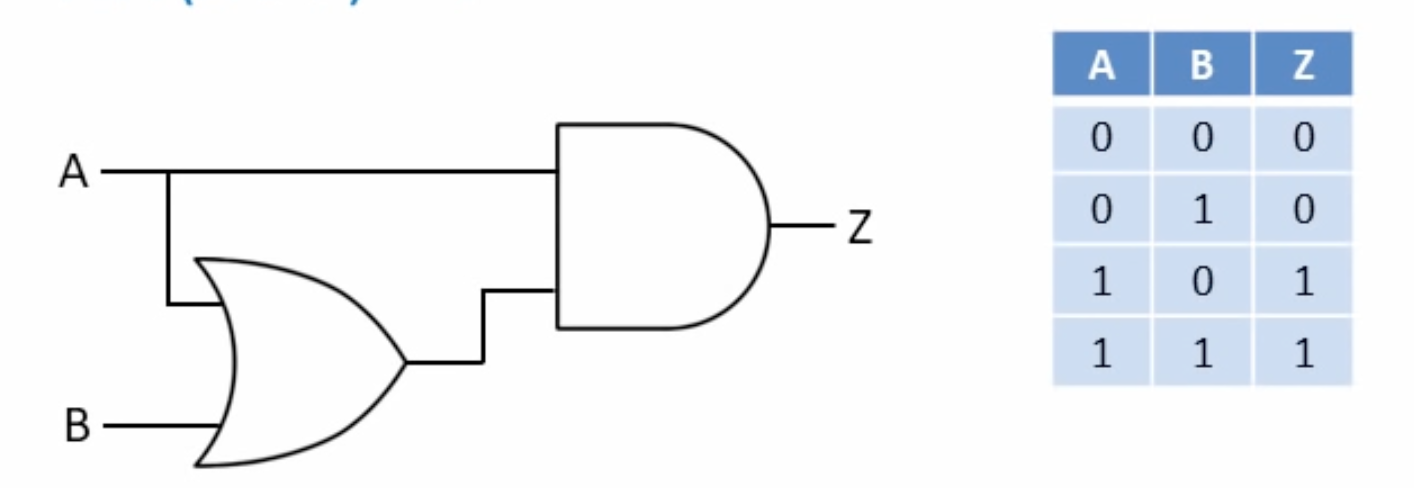
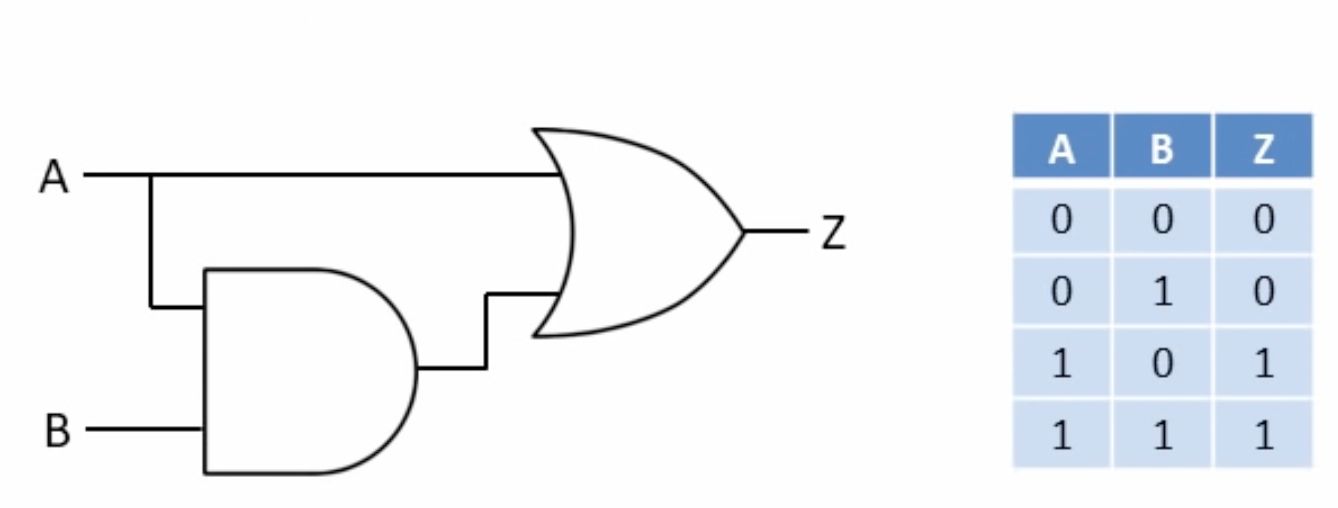
10- De Morgan's Laws

1- The complement of the product of two variables equals the sum of their complements.

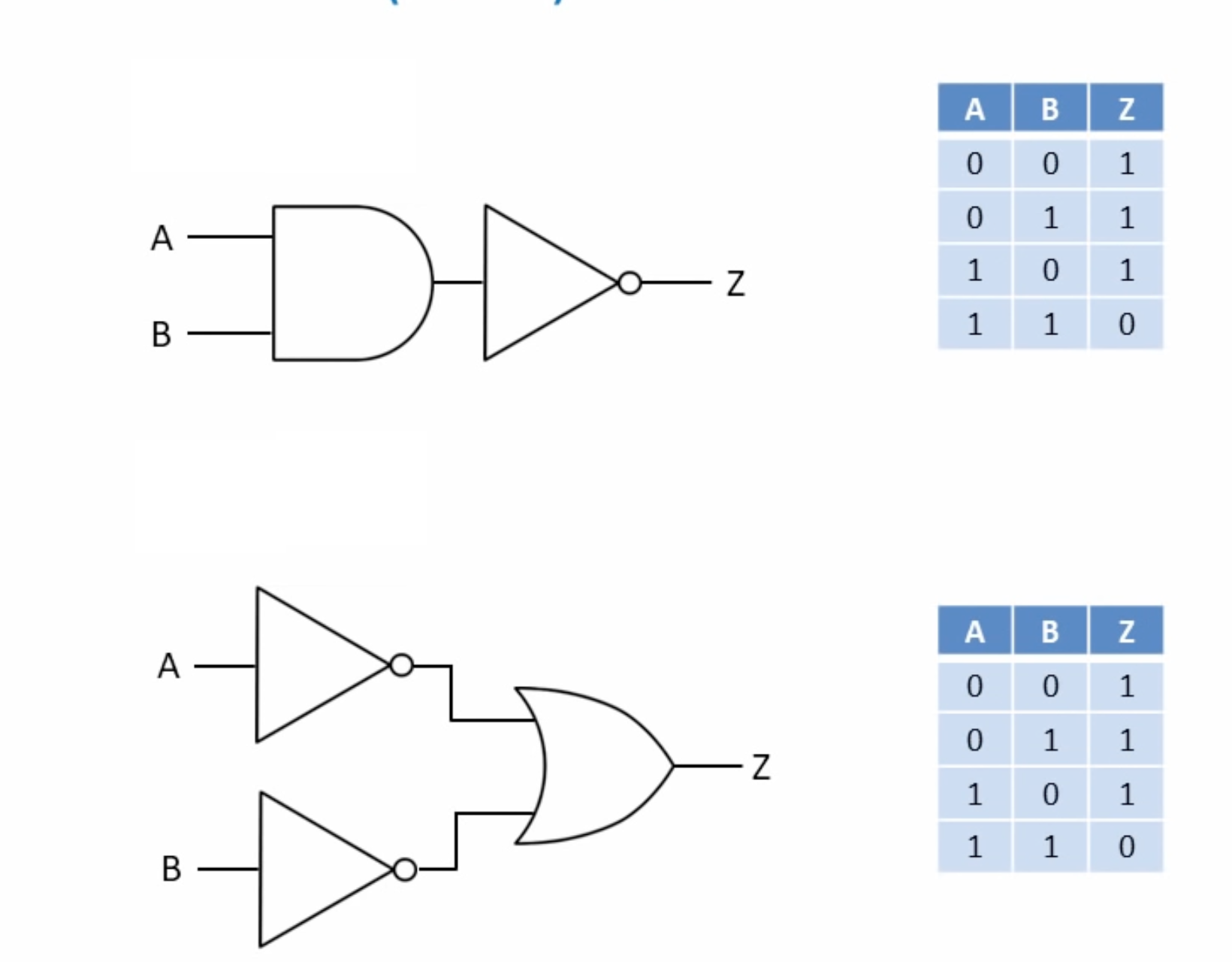
10- De Morgan's Laws (Cont'd)

2- The complement of the sum of two variables equals the product of their complements.

Q: How to get True?

1. F= AB+1+CD =?

2. F=A.B.0.C.D =?

Reduction of Gates

• If we can reduce the number of gate and yet produce the
  same functionality we gain the benefits of:

  • Economy
  • Speed
  • Increased ability

Minimise using laws

A literal by itself cancels out any term that contains it: (Absorption)

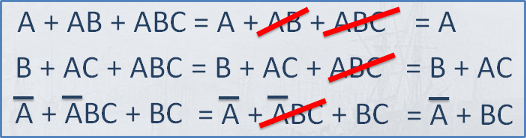
Minimise using laws

A literal by itself knocks out its not’ed opposite that appears in any minterm (Absorption)

Minimise using laws

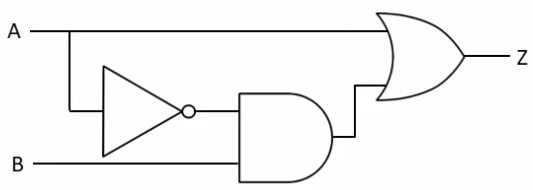
Soluting

Step 1: Apply Distributive Law

Step 2: Apply Complement Identity)

= 1 . (A + B)

Step 3: Apply Identity Law
Z = 1 . (A + B)
= A + B

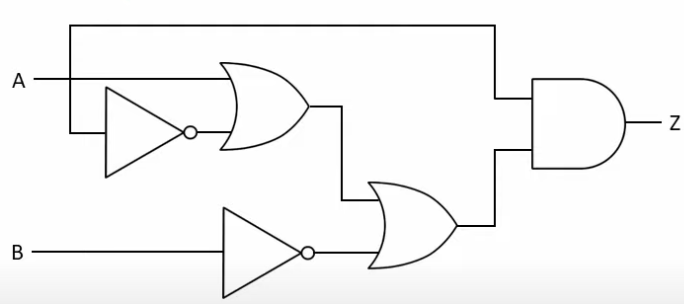
Soluting

Step 1: Apply Complement Law

Step 2: Apply Annulment Law

Step 3: Apply identity Law

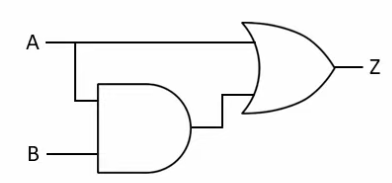
Soluting

• Apply Distributive Law

• Use Idempotent Law (Twice)

• Again use Idempotent and Associative Law

• Use Distributive Law

Soluting

• Z = A + (A . B) // Brackets for clarity

• Use Identity Law : A + 1 = A
  Z = (A + 1) + (A . B)

• Distributive law - factorise
  Z = A + (1 . B)

• Annulment law: A + 1 = 1
  Z = A + 1

• Identity law: A . 1 = A
  Z = A

Summary

• A literal is a boolean variable or its complement.
• A product term (also known as minterm) is the product of literals.
• Two or more product terms are summed by Boolean addition; the resulting expression is a sum-of-products (SOP).
• A truth table is simply a list of the possible combinations of input variable values and the corresponding output values.
• Output of a logic circuit is written as a Boolean sum of product of only those cases where a circuit produces a 1.
• To reduce cost and increase speed of computing device, we need to minimize the circuit.
• Apply basic rules of Boolean Algebra for circuit minimization.

Lab

• Link to the lab
• You can also review the following:
  • This book (from Page 147)
  • And this book too, (from page B-6)